2020/01/23
支持向量机(Support vector machines)
一、简介
支持向量机(support vector machines)是一种二分类模型,它的目的是寻找一个超平面来对样本进行分割,分割的原则是间隔最大化,最终转化为一个凸二次规划问题来求解。由简至繁的模型包括:
- 当训练样本线性可分时,通过硬间隔最大化,学习一个线性可分支持向量机;
- 当训练样本近似线性可分时,通过软间隔最大化,学习一个线性支持向量机;
- 当训练样本线性不可分时,通过核技巧和软间隔最大化,学习一个非线性支持向量机;
与逻辑回归和神经网络相比,支持向量机,或者简称SVM,在学习复杂的非线性方程时提供了一种更为清晰,更加强大的方式。
二、SVM 与 Logistic regression
逻辑回归预测函数:
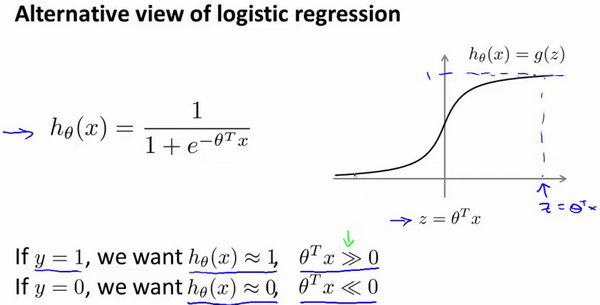
现在考虑下我们想要逻辑回归做什么:
当 y=1 时, 我们需要预测函数 h(x)≈1, 需要 Z >= 0
当 y=0 时, 我们需要预测函数 h(x)≈0, 需要 Z <= 0
则对应的代价函数(z = theta.T * x)
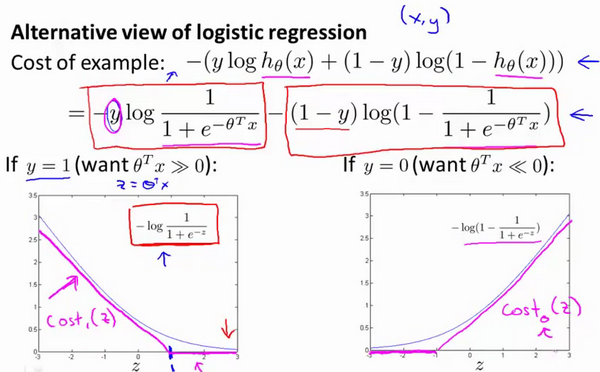
当y值不同时,J(z)函数的曲线可大致拟合成一条折线cost(z)。将逻辑回归中J(z)替换为拟合的这条折线cost(z),我们得到一个新的最小化函数:
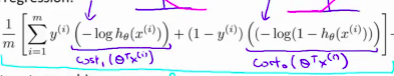
加入正则项,再让其在逻辑回归代价函数上面稍加变形,则得到了SVM的函数:
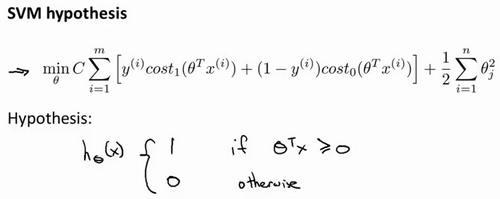
最后有别于逻辑回归输出的概率。在这里,我们的代价函数,当最小化代价函数,获得参数theta时,支持向量机所做的是它来直接预测y的值等于1,还是等于0。
三、SVM
人们有时将支持向量机看作是大间距分类器。在训练得到最小化的theta过程中,先忽略参数C和正则项,则theta的变化方向是使得
当 y=1 时, z>= 1 ,当 y=0 时, z<=-1 (而不是逻辑回归中的0) 
如果你考察这样一个数据集,其中有正样本,也有负样本,可以看到这个数据集是线性可分的。我的意思是,存在一条直线把正负样本分开。当然有多条不同的直线,可以把正样本和负样本完全分开。
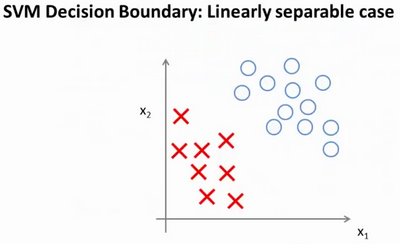
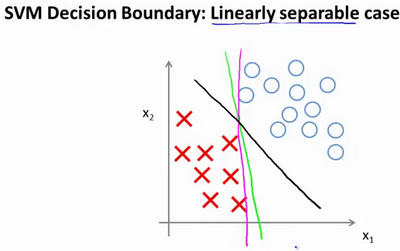
这些决策边界看起来都不是特别好的选择,支持向量机将会选择这个黑色的决策边界,相较于之前我用粉色或者绿色画的决策界。这条黑色的看起来好得多,黑线看起来是更稳健的决策界。在分离正样本和负样本上它显得的更好。数学上来讲,这是什么意思呢?这条黑线有更大的距离,这个距离叫做间距(margin)。
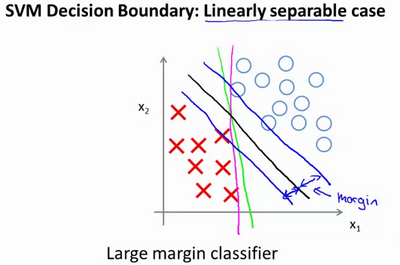
当画出这两条额外的蓝线,我们看到黑色的决策界和训练样本之间有更大的最短距离。然而粉线和蓝线离训练样本就非常近,在分离样本的时候就会比黑线表现差。因此,这个距离叫做支持向量机的间距,而这是支持向量机具有鲁棒性的原因,因为它努力用一个最大间距来分离样本。因此支持向量机有时被称为大间距分类器。
参数C对划分的影响:
- C较大时,可能会导致过拟合,高方差
- C较小时,可能会导致欠拟合,高偏差
例如:当 C较小时会得到黑线,而增大C使得C非常大时,会得到粉色线
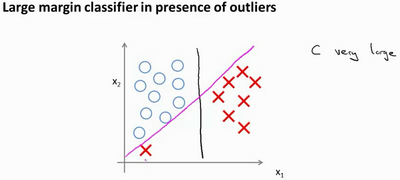
关于SVM如何做到大间距分类这里先不解释。
四、核函数
许多时候,我们面临的分类问题并不只是线性分类,还会遇到很多无法通过直线进行分隔的分类情况:
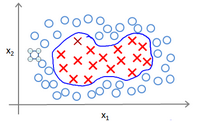
我们可以用一系列的新的特征f来替换模型中的每一项。将f代替x来对进行分类。而这个代替的变化函数则叫做核函数。例如:
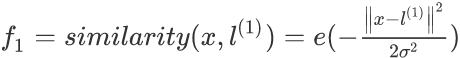
这是一个高斯核函数(Gaussian Kernel)。其中l为landmark,为数据中的地标,使用数据与地标的距离大小计算用来取新的特征,距离越大获得的f值则越小,当距离为0时,f达到最大为1。例如在坐标中取3个地标:
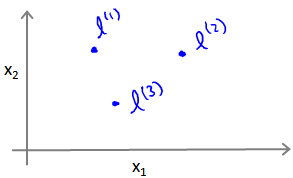
这样得到的新特征与地标相关系,关联到数据与地标间的欧式距离,而训练出的theta也会通过这个核函数得到复杂的拟合边界。
其中高斯核函数中的参数 sigma 为用户定义的到达率,为核函数跌至0的速率参数
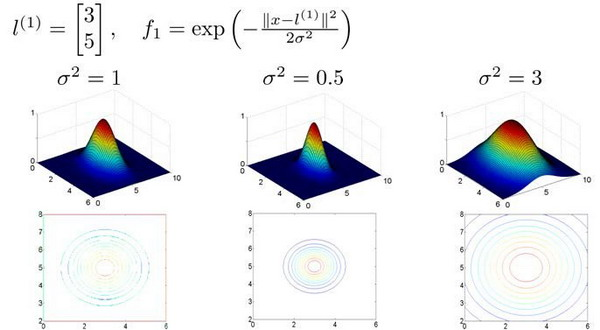
一般实现核函数SVM时使用的地标为整个数据集,即如果训练集有m个样本,则选取m个地标。

两个参数 C 和 sigma 的影响
C较大时,可能会导致过拟合,高方差
C较小时,可能会导致欠拟合,高偏差
sigma 较大时,可能导致低方差,高偏差 (欠拟合)
sigma 较小时,可能导致低偏差,高方差 (过拟合)
除了高斯核函数外,还有很多其他的核函数,这里不一一介绍了。
这里只是初步对 SVM 作介绍和一些使用方法,其数学原理将在后续补充。
了解更多人工智能方面欢迎光顾个人博客: 戴挽舟的博客


