在训练机器学习模型寻找最优函数时,梯度下降(Gradient Descent)是最常用的优化(optimization)方法。在给定一组初始参数θ0时,梯度下降算法能够顺着损失函数下降最快的方向逐步逼近最低点,也就是最佳参数θ∗的位置。那梯度下降算法为什么work呢?为什么梯度的反方向就是损失函数下降最快的方向呢?
梯度下降算法解释
首先回顾一下梯度下降算法是如何工作的,我们的目标是找到θ∗:
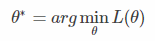
其中LL是损失函数,梯度下降算法步骤如下:
1.随机选取一组初始参数θ0。
2.计算损失函数在该点的偏导数∇L(θ^(n−1)),也就是梯度。
3.更新参数θn=θn−1−η∇L(θn−1)。
4.重复2,3步骤,直至梯度不再下降(小于某个阈值范围)。
上面第3步中可以看到,每次我们顺着梯度的反方向更新θ,其中η是学习速率,代表了每次更新的步伐大小。在只含有两个未知参数时,梯度下降的直观过程如下图: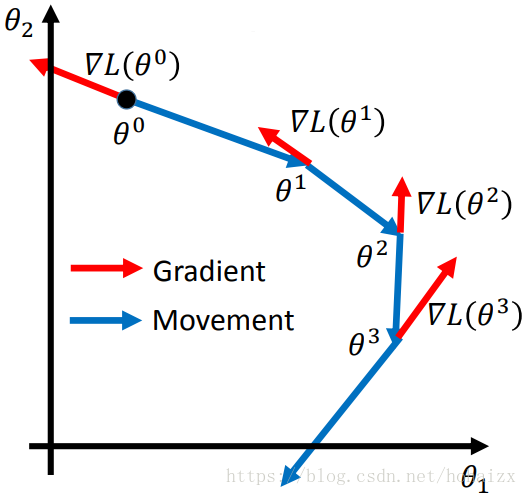
下面根据李宏毅课程的思路对梯度下降的原理进行解释。同样假设只包含两个参数θ1,θ2。随机给定一个初始点,在“目之所及”的范围内寻找损失函数下降最快的方向,如下图
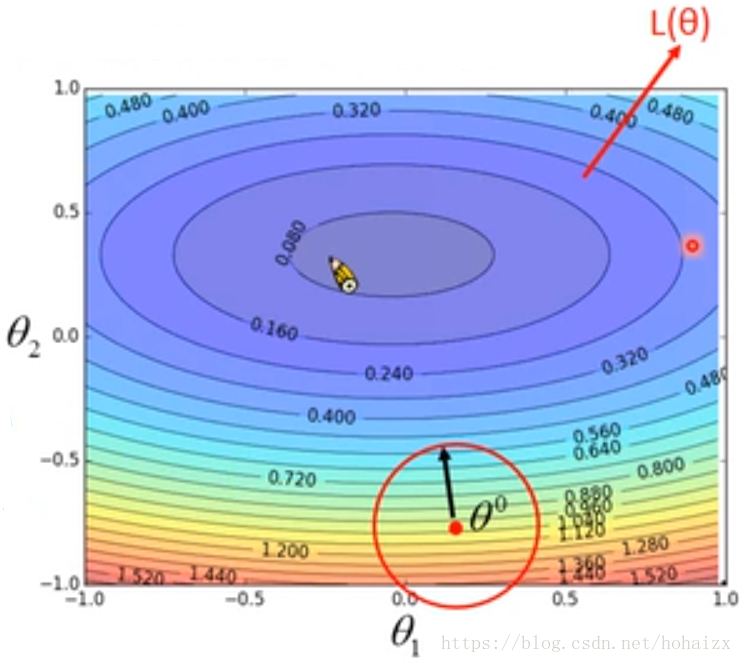
θ0是随机给定的初始点,红色圆圈是“目之所及”的范围,现在的关键是如何找到圆圈范围内下降最快的方向,由泰勒展示(Taylor Series):当函数h(x)在x=x0处是可微的,那么h(x)可以写成
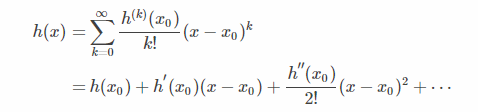
当x非常接近x0时,上式中的平方项等更高次项的值将无限接近于0,此时h(x)可以约等于
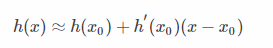
多变量泰勒展示同样成立,只需对各个变量分别求偏导数
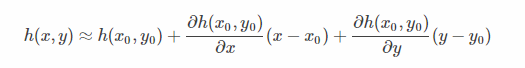
因此,在任意点(a,b)处我们可以将损失函数用泰勒展示展开,并且当红色圆圈足够小时,圆圈内的函数值可以近似为 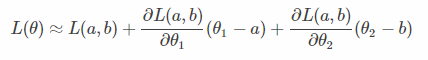


经过上面的推导,我们很好的解释了为什么要沿着梯度的反方向更新参数,并且也解释了学习速率ηη不能设置过大,否则L(θ)≈s+uΔθ1+vΔθ2将不再成立。
梯度下降的一些技巧
1、学习速率(learning rate)
学习速率是最需要调整的一个超参数,太小会使得训练速度过慢;太大会使得训练无法收敛,因此需要很小心的调节学习速率η。
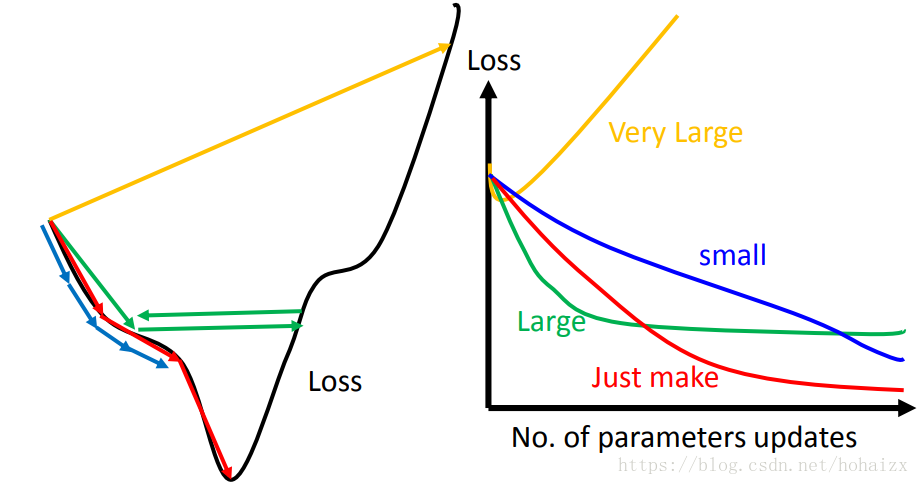
我们可以绘出损失函数的曲线图,如上图左边所示,红色的学习速率最合适,蓝色的太小,绿色的偏大,黄色则非常大。但是当参数数目很多时将无法可视化损失函数曲线,这时我们可以绘制出随迭代次数增加损失值变化曲线,如上图右边所示。如果损失下降很慢(蓝色),可能学习速率过低;如果损失开始下降很快,但很快稳定在一个较大的值(绿色),可能学习速率偏大了;如果损失不降返升(黄色),学习速率可能过大了;只有损失以恰当的速度降到很小(红色),才是最佳学习速率。
2、Adagrad

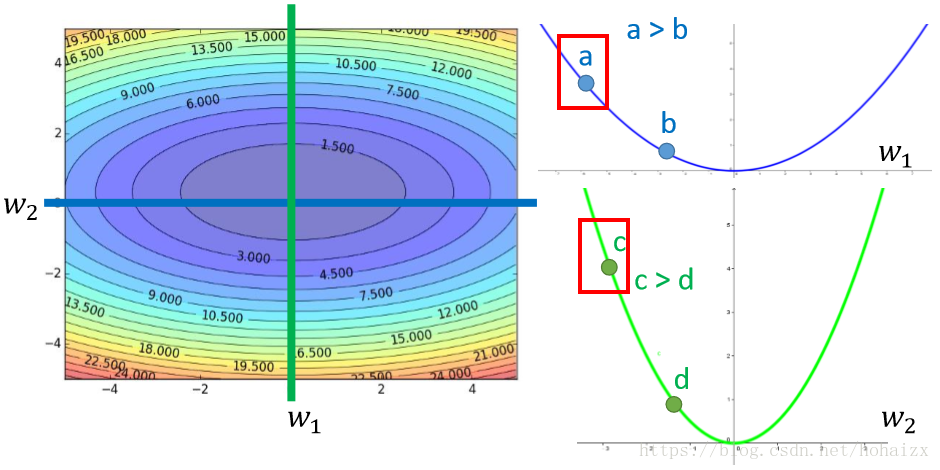
下面尝试对Adagrad做一个解释,首先需要考虑的是:梯度越大,距离最低点越远,步伐越大?还是以两参数为例:

3、随机梯度下降(Stochastic Gradient Descent)or 小批量梯度下降(Mini-Batch Gradient Descent)
常规的梯度下降也就是批量梯度下降,是在整个数据集上求偏导,在该方法中,每次更新我们需要计算整个数据集中每个样本点的误差,因此速度会比较慢,对于很大的数据集,内存可能无法容纳以至无法使用,因此在实际中一般使用随机梯度下降(Stochastic Gradient Descent)或者小批量梯度下降(Mini-Batch Gradient Descent)。随机梯度下降(Stochastic Gradient Descent)的每次更新,是对数据集中的每个样本点计算损失函数,这样对于m个样本的数据集,批量梯度下降更新一次,SGD可以更新m次,虽然每次只考虑一个样本点,可能存在较大的波动,但最终都会收敛。小批量梯度下降(Mini-Batch Gradient Descent)是批量梯度下降和随机梯度下降的折中,每次更新,对数据集中部分数据计算损失函数。
4、特征缩放(Feature Scaling)
特征缩放是指将每个特征的取值限定在相同的范围

为什么要将每个特征的取值限定在相同范围呢?看下面的例子:

图中左边x1的取值范围是x2的百分之一,当w2稍有变化,y值将变化很大,因此损失函数也将变化很大,也就是说损失函数在w2方向下降很快,导致损失函数等高线呈扁平的椭圆形,这种情况下不用Adagrad将比较难处理,两个方向上需要不同的学习率。但经过特征缩放后,所有特征的取值范围都是统一的,损失函数等高线呈规整的圆形,梯度下降效率将比较高。


