从Lentet-5看CNN

卷积

首先我们用一个$3 \times 3$的核对一个$6 \times 6$的矩阵进行卷积运算，会得到一个$4 \times 4$的矩阵

我们把核映射到矩阵上对应相乘相加，比如$4 \times 4$矩阵的第一个元素-5

但是我们也得知卷积会使矩阵变小

其中在tensorflow中可以使用tf.nn.conv2d()

tf.nn.conv2d(
    input,
    filters,
    strides,
    padding,
    data_format='NHWC',
    dilations=None,
    name=None
)

其中卷积可以用于边缘检测，如图

因为$3\times3$的矩阵太小使用边缘比较粗

由此可见上面的卷积都使原图像的大小变小了，为了使大小不变，我们使用了提高padding（即在原图像边缘填充像素）

设源图像大小为$n \times n$,卷积核为$f \times f$，padding为p，所以卷积后图像大小为$[(n+2p-f+1) \times (n+2p-f+1)]$。

同时我们引入步长这一个概念（即卷积核每次移动的单位长度）。

设源图像大小为$n \times n$,卷积核为$f \times f$，padding为p，步长为s，所以卷积后图像大小为$[(\frac{n+2p-f}{s}+1) \times (\frac{n+2p-f}{s}+1)]$。

如果第L层是卷积层：

其中：

$f^{[l]}$:卷积核大小

$p^{[l]}$:填充大小

$s^{[l]}$:步长大小

$n^{[l]}_c$:卷积层数目

输入：$n^{[l-1]}_H\times n^{[l-1]}_W\times n^{[l-1]}_c$

输出:$n^{[l]}_H\times n^{[l]}_W\times n^{[l]}_c$

每个卷积核 :$f^{[l]}\times f^{[l]}\times f_c^{[l-1]}$

激活函数:$a^{[l]}\to n^{[l]}_H\times n^{[l]}_W\times n^{[l]}_c$

权重:$f^{[l]}\times f^{[l]}\times n_c^{[l-1]}\times n_c^{[l-1]}$

偏差：$n_c^{[l]}-(1,1,1,n_c^{[l]})$

卷积神经网络的结构

一般卷积神经网络是由输入层、卷积层、激活层、池化层、全连接层、输出层组成

输入层

输入层要进行数据的预处理，比如去均值、归一化、PCA/SVD降维等

卷积层

卷积层主要通过对每一个局部感知，然后更高层次的局部感知，最终得到全局信息。

其中卷积有两个大杀器一个是局部感知野，另一个是权值共享。

局部感知野

如果我们有1000x1000像素的图像，有1百万个隐层神经元，那么他们全连接的话（每个隐层神经元都连接图像的每一个像素点），就有1000x1000x1000000=10^12^个连接，也就是10^12^个权值参数。

图像的空间联系也是局部的像素联系较为紧密，而距离较远的像素相关性则较弱。因而，每个神经元其实没有必要对全局图像进行感知，只需要对局部进行感知，然后在更高层将局部的信息综合起来就得到了全局的信息。图像的空间联系是局部的，就像人是通过一个局部的感受野去感受外界图像一样，每一个神经元都不需要对全局图像做感受，每个神经元只感受局部的图像区域，然后在更高层，将这些感受不同局部的神经元综合起来就可以得到全局的信息了

假如局部感受野是10x10，就有10x10x1000000=10^8^个连接减少了4个数量级，也就是减少了4个数量级的参数

权值共享

假如使用一个卷积层，参数都是一样的，那只能提取一个特征了，我们总需要提取多个特征的啊，那我们就加多个卷积，每个卷积层不同。那么隐层的神经元个数怎么确定呢？它和原图像，也就是输入的大小（神经元个数）、滤波器的大小和滤波器在图像中的滑动步长都有关。

池化层

1. 降维，减少网络要学习的参数数量
2. 防止过拟合
3. 扩大感受野
4. 实现不变性（平移、旋转、尺度不变性）

Lenet-5

下面我们从著名的神经网络Lenet-5来看卷积

paper地址

效果图：

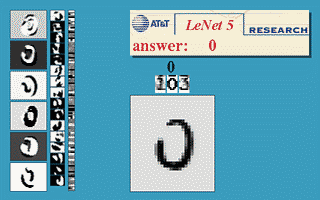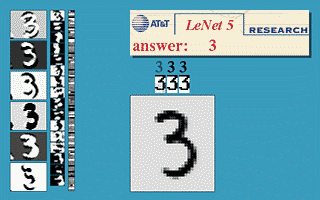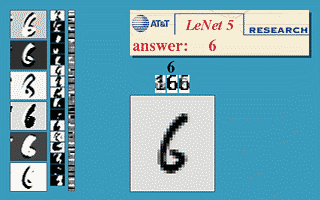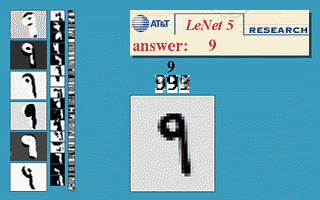
上图包含输入层总共8层网络，分别为：输入层（INPUT）、卷积层（Convolutions,C1）、池化层（Subsampling，S2）、卷积层（C3）、池化层（Subsampling，S4）、卷积层（C5）、全连接层（F6）、输出层（径向基层）

卷积和子采样过程：卷积过程包括：用一个可训练的滤波器fx去卷积一个输入的图像（第一阶段是输入的图像，后面的阶段就是卷积特征map了），然后加一个偏置bx，得到卷积层Cx。子采样过程包括：每邻域四个像素求和变为一个像素，然后通过标量Wx+1加权，再增加偏置bx+1，然后通过一个sigmoid激活函数，产生一个大概缩小四倍的特征映射图Sx+1。

我们输入32x32的图像经过6通道的5x5的卷积后，特征图为28x28，其中C1的训练参数个数是(5x5+1)x6=156，连接数是156x(28x28)=122304。其中5x5是卷积核大小为5x5，+1个偏置单元，6个通道。

其中S2是一个下采样层，利用图像局部相关性的原理，对图像进行子抽样，可以减少数据处理量同时保留有用信息，其中C1通过下采样层得到一个14x14的特征图，其中14x14的特征图的每一个单元与C1中的与之相对应的2x2的邻域有关。C1层每个单元的4个输入相加，乘以一个可训练参数，再加上一个可训练偏置。结果通过sigmoid函数计算。如果系数比较小，那么运算近似于线性运算，亚采样相当于模糊图像。如果系数比较大，根据偏置的大小亚采样可以被看成是有噪声的“或”运算或者有噪声的“与”运算。每个单元的2x2感受野并不重叠，因此S2中每个特征图的大小是C1中特征图大小的1/4（行和列各1/2）。其中S2的训练参数是(1x1+1)x6=12，连接数是(2x2+1)x6x(14x14)=5880

用一个16通道的5x5的卷积核去卷积S2可以得到C3，其大小为10x10的16通道的一个特征图，其中C3中的每个特征map是连接到S2中的所有6个或者几个特征map的，表示本层的特征map是上一层提取到的特征map的不同组合。

如上图，横向的数表示卷积层C3的特征平面，纵向表示池化层的6个采样平面，我们以卷积层C3的第0号特征平面为例，它对应了池化层的前三个采样平面即0,1,2，三个平面使用的是三个卷积核（每个采样平面是卷积核相同，权值相等，大小为5x5）,既然对应三个池化层平面，那么也就是说有5x5x3个连接到卷积层特征平面的一个神经元，因为池化层所有的样本均为14x14的，而卷积窗口为5x5的，因此卷积特征平面为10x10（大家可按照第一个卷积计算求的）。只是这里的卷积操作要更复杂，他不是所有的都是特征平面对应三个池化层平面，而是变化的，从上图我们可以清楚的看到前6个特征平面对应池化层的三个平面即0,1,2,3,4,5 ， 而6~14每张特征平面对应4个卷积层，此时每个特征平面的一个神经元的连接数为5x5x4，最后一个特征平面是对应池化层所有的样本平面，

连接数： (5x5x3+1)x10x10x6+(5x5x4+1)x10x10x9+(5x5x6+1)x10x10 = 45600+90900+15100=151600

权值数： (5x5x3+1)x6 + (5x5x4+1)x9 + 5x5x6+1 = 456 + 909+151 = 1516

S4层是一个下采样层，由16个5x5大小的特征图构成。特征图中的每个单元与C3中相应特征图的2x2邻域相连接，跟C1和S2之间的连接一样。S4层有(1x1+1)x16=32个可训练参数（每个特征图1个因子和一个偏置）和(2x2+1)x16x(5x5)=2000个连接。

原因有两方面：采用非连接的方案将连接数保持在合理的范围内，而且破坏了神经网络的对称性（我也没太理解清楚。。。）

C5是卷积层。。。

好像是用一个120个通道的5x5的卷积核与S4做卷积，正好构成全连接的关系。（以上是个人猜测）

目前我也没搞懂。。。先留着

F6有84个单元，因为在计算机中字符的编码是ASCII编码，这些图是用7x12大小的位图表示的，也就是高宽比为7:12，如下图，选择这个大小可以用于对每一个像素点的值进行估计。

这一层其实就是BP网络的隐层，且为全连接层，即这一层有84个神经元，每一个神经元都和上一次的120个神经元相连接，那么连接数为(120+1)x84 = 10164,因为权值不共享，隐层权值数也是10164，至于为什么隐层是84个神经元稍后解释，本层的输出有激活函数，激活函数为双曲正切函数：

根据论文解释：A的幅值，S是原点处的倾斜率，A的经验值是1.7159，原因没说。

输出层：有10个输出，对应0-9的数字

首先大家应该明白什么是径向基神经网络，他基于距离进行衡量两个数据的相近程度的，RBF网最显著的特点是隐节点采用输人模式与中心向量的距离（如欧氏距离）作为函数的自变量，并使用径向基函数（如函数）作为激活函数。径向基函数关于N维空间的一个中心点具有径向对称性，而且神经元的输人离该中心点越远，神经元的激活程度就越低。上式是基于欧几里得距离，怎么理解那个式子呢？就是说F6层为84个输入用$x_j$表示，而输出有10个用$y_i$表示，而权值使用$w_{ji}$表示，上式说明所有输入和权值的距离平方和为依据判断，如果越相近距离越小，输出越小则去哪个，如果我们存储的到$w_{ji}$的值为标准的输出，如标准的手写体0,1,2,3等，那么最后一层就说明。F6层和标准的作比较，和标准的那个图形越相似就说明就越是那个字符的可能性更大。

卷积神经网络关于感受野的计算

什么是感受野

在计算机视觉领域的深度神经网络中有一个概念叫做感受野，用来表示网络内部的不同位置的神经元对原图像的感受范围的大小。

白话版：感受野（Receptive Field），指的是神经网络中神经元“看到的”输入区域，在卷积神经网络中，feature map上某个元素的计算受输入图像上某个区域的影响，这个区域即该元素的感受野。

神经元之所以无法对原始图像的所有信息进行感知，是因为在这些网络结构中普遍使用卷积层和pooling层，在层与层之间均为局部相连（通过sliding filter）。神经元感受野的值越大表示其能接触到的原始图像范围就越大，也意味着他可能蕴含更为全局、语义层次更高的特征；而值越小则表示其所包含的特征越趋向于局部和细节。因此感受野的值可以大致用来判断每一层的抽象层次。

可以看到在Conv1中的每一个单元所能看到的原始图像范围是3*3，而由于Conv2的每个单元都是由 范围的Conv1构成，因此回溯到原始图像，其实是能够看到 的原始图像范围的。因此我们说Conv1的感受野是3，Conv2的感受野是5. 输入图像的每个单元的感受野被定义为1，这应该很好理解，因为每个像素只能看到自己。

感受野的计算

K：卷积核大小

P：填充块大小

S：步长

Layer：用Layer表示 (特征图)feature map，特别地Layer 0为输入图像

n：特征图的大小

r：感受野大小

j：特征图上相邻的像素距离，即：在特征图上前进1步相当于输入图像上前进多少个像素

如下图所示，feature map上前进1步，相当于输入图像上前进2个像素，𝑗=2

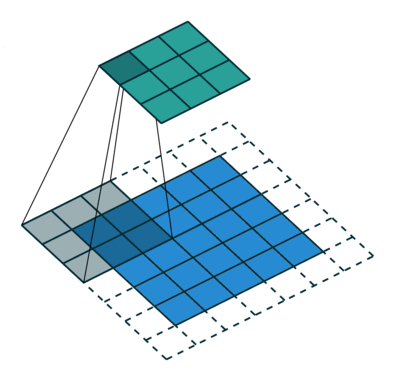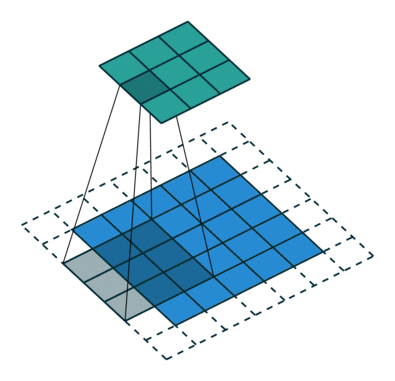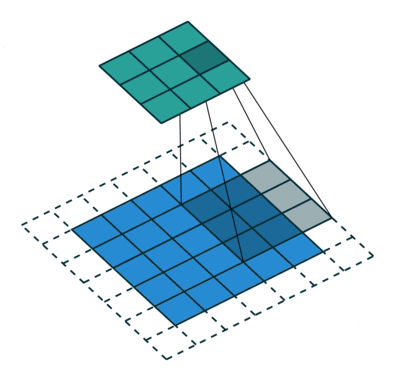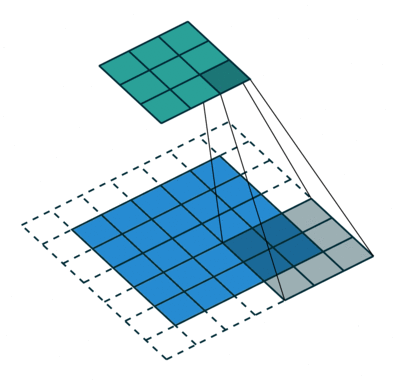
start：在特征图左上角第一个像素在输入图像上的感受野中心坐标。

在上图中，左上角绿色块感受野中心坐标为(0.5,0.5)，即左上角蓝色块中心的坐标，左上角白色虚线块中心的坐标为(−0.5,−0.5)；

再看上面的动图，如果feature map Layer2 上的一个元素A看到feature map 𝐿𝑎𝑦𝑒𝑟 1上的范围为3×3（图中绿色块），其大小等于kernel size $𝑘_2$，所以，A看到的感受野范围$r_2$等价于Layer 1上3×3窗口看到的Layer 0 范围，据此可以建立起相邻Layer感受野的关系，如下所示，其中$r_{l-1}$为Layer l-1的感受野，$r_l−1$为Layer l−1 的感受野，
$$
𝑟_𝑙=𝑟_{𝑙−1}+(𝑘_𝑙−1)\times 𝑗_𝑙−1
$$

• 𝐿𝑎𝑦𝑒𝑟 𝑙 一个元素的感受野𝑟𝑙等价于𝐿𝑎𝑦𝑒𝑟 𝑙−1上𝑘×𝑘个感受野的叠加；
• 𝐿𝑎𝑦𝑒𝑟 𝑙−1上一个元素的感受野为$r_{l−1}$；
• 𝐿𝑎𝑦𝑒𝑟 𝑙−1上连续𝑘k 个元素的感受野可以看成是，第1个元素看到的感受野加上剩余k−1步扫过的范围，𝐿𝑎𝑦𝑒𝑟 𝑙−1 上每前进1个元素相当于在输入图像上前进$𝑗_{𝑙−1}$个像素，结果等于$𝑟_{𝑙−1}+(𝑘−1)×𝑗_{𝑙−1}$

感受野中心

感受野小结

关于卷积神经网络的部分代码

二维卷积

def corr2d(X, K):  
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1)) # 卷积输出的图像大小
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i: i + h, j: j + w] * K).sum()
    return Y

多输入通道

def corr2d_multi_in(X,K):
    # 沿着X和K的第0维（通道维）分别计算再相加
    res = corr2d(X[0, :, :], K[0, :, :])
    for i in range(1, X.shape[0]):
        res += corr2d(X[i, :, :], K[i, :, :])
    return res

X = torch.tensor([[[0, 1, 2], 
                   [3, 4, 5],
                   [6, 7, 8]],
                  [[1, 2, 3],
                   [4, 5, 6],
                   [7, 8, 9]]])
K = torch.tensor([[[0, 1],
                   [2, 3]],
                  [[1, 2],
                   [3, 4]]])

print(X.size())
print(K.size())
print(corr2d_multi_in(X, K))
print([k for k in K])

多输出通道

def corr2d_multi_in_out(X, K):
    # 对K的第0维遍历，每次同输入X做互相关计算。所有结果使用stack函数合并在一起
    return torch.stack([corr2d_multi_in(X, k) for k in K])

K=torch.stack([K,K+1,K+2])
print(K.shape)

print(corr2d_multi_in_out(X,K))

1x1卷积层

def corr2d_multi_in_out_1x1(X,K):
    c_i,h,w=X.shape
    c_o=K.shape[0]
    X=X.view(c_i,h*w)
    print('X.view(',c_i,',',h*w,'):\n',X)
    K=K.view(c_o,c_i)
    print('K.view(',c_o,',',c_i,'):\n',K)
    Y=torch.mm(K,X)
    return Y.view(c_o,h,w)
    
X=torch.rand(3,3,1)
K=torch.rand(2,3,1,1)

print('X:\n',X)
print(X.size())
print('K:\n',K)
print(K.size())

Y1=corr2d_multi_in_out_1x1(X,K)
Y2=corr2d_multi_in_out(X,K)

print((Y1-Y2).norm().item()<1e-6)

最大池化层和ping

def pool2d(X, pool_size, mode='max'):
    X=X.float()
    p_w,p_h=pool_size
    Y=torch.zeros(X.shape[0]-p_h+1,X.shape[1]-p_w+1)
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode=='max':
                Y[i,j]=X[i:i+p_h,j:j+p_w].max()
            if mode=='avg':
                Y[i,j]=X[i:i+p_h,j:j+p_w].mean()
    return Y

X=torch.tensor([[0,1,2],
                [3,4,5],
                [6,7,8]])
print(pool2d(X,(2,2)))

print(pool2d(X,(2,2),mode='avg'))

填充和步幅

x=torch.arange(16).view(1,1,4,4)
print(x)

Lenet-5

class LeNet(nn.Module):
    def __init__(self):
        super(LeNet,self).__init__()
        self.conv=nn.Sequential(
            nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
            nn.Sigmoid(),
            nn.MaxPool2d(2,2), # kernel_size, stride
            nn.Conv2d(6,16,5),
            nn.Sigmoid(),
            nn.MaxPool2d(2,2)
        )
        self.fc=nn.Sequential(
            nn.Linear(16*4*4,120),
            nn.Sigmoid(),
            nn.Linear(120,84),
            nn.Sigmoid(),
            nn.Linear(84,10)
        )
    
    def forward(self, img):
        feature=self.conv(img)
        output=self.fc(feature.view(img.shape[0],-1))
        return output

net=LeNet()
print(net)

def load_data_fashion_mnist(batch_size, resize=None, root='./data'):
    """Download the fashion mnist dataset and then load into memory."""
    trans = []
    if resize:
        trans.append(torchvision.transforms.Resize(size=resize))
    trans.append(torchvision.transforms.ToTensor()) # 将PIL image或numpy.darray 转化成tensor

    transform = torchvision.transforms.Compose(trans)
    mnist_train = torchvision.datasets.FashionMNIST(root=root, train=True, download=True, transform=transform)
    mnist_test = torchvision.datasets.FashionMNIST(root=root, train=False, download=True, transform=transform)

    train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=4)
    test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=4)

    return train_iter, test_iter

batch_size = 128
# 如出现“out of memory”的报错信息，可减小batch_size或resize
train_iter, test_iter = load_data_fashion_mnist(batch_size, resize=224)

batch_size = 256
train_iter, test_iter = load_data_fashion_mnist(batch_size=batch_size)

def evaluate_accuracy(data_iter, net, device=None):
    if device is None and isinstance(net, torch.nn.Module):
        # 如果没指定device就使用net的device
        device = list(net.parameters())[0].device
    acc_sum, n = 0.0, 0
    with torch.no_grad():
        for X, y in data_iter:
            if isinstance(net, torch.nn.Module):
                net.eval() # 评估模式, 这会关闭dropout
                acc_sum += (net(X.to(device)).argmax(dim=1) == y.to(device)).float().sum().cpu().item()
                net.train() # 改回训练模式
            else: 
                if('is_training' in net.__code__.co_varnames): # 如果有is_training这个参数
                    # 将is_training设置成False
                    acc_sum += (net(X, is_training=False).argmax(dim=1) == y).float().sum().item() 
                else:
                    acc_sum += (net(X).argmax(dim=1) == y).float().sum().item() 
            n += y.shape[0]
    return acc_sum / n

def train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs):
    net = net.to(device)
    print("training on ", device)
    loss = torch.nn.CrossEntropyLoss()
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n, batch_count, start = 0.0, 0.0, 0, 0, time.time()
        for X, y in train_iter:
            X = X.to(device)
            y = y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            optimizer.zero_grad()
            l.backward()
            optimizer.step()
            train_l_sum += l.cpu().item()
            train_acc_sum += (y_hat.argmax(dim=1) == y).sum().cpu().item()
            n += y.shape[0]
            batch_count += 1
        test_acc = evaluate_accuracy(test_iter, net)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f, time %.1f sec'
              % (epoch + 1, train_l_sum / batch_count, train_acc_sum / n, test_acc, time.time() - start))

lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)