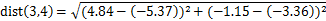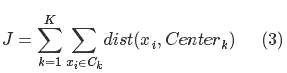1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
|
import numpy as np
import matplotlib.pyplot as plt
def loadDataSet(fileName):
data = np.loadtxt(fileName,delimiter='\t')
return data
def distEclud(x,y):
return np.sqrt(np.sum((x-y)**2))
def randCent(dataSet,k):
m,n = dataSet.shape
centroids = np.zeros((k,n))
for i in range(k):
index = int(np.random.uniform(0,m))
centroids[i,:] = dataSet[index,:]
return centroids
def KMeans(dataSet,k):
m = np.shape(dataSet)[0]
clusterAssment = np.mat(np.zeros((m,2)))
clusterChange = True
centroids = randCent(dataSet,k)
while clusterChange:
clusterChange = False
for i in range(m):
minDist = 100000.0
minIndex = -1
for j in range(k):
distance = distEclud(centroids[j,:],dataSet[i,:])
if distance < minDist:
minDist = distance
minIndex = j
if clusterAssment[i,0] != minIndex:
clusterChange = True
clusterAssment[i,:] = minIndex,minDist**2
for j in range(k):
pointsInCluster = dataSet[np.nonzero(clusterAssment[:,0].A == j)[0]]
centroids[j,:] = np.mean(pointsInCluster,axis=0)
print("Congratulations,cluster complete!")
return centroids,clusterAssment
def showCluster(dataSet,k,centroids,clusterAssment):
m,n = dataSet.shape
if n != 2:
print("数据不是二维的")
return 1
mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr']
if k > len(mark):
print("k值太大了")
return 1
for i in range(m):
markIndex = int(clusterAssment[i,0])
plt.plot(dataSet[i,0],dataSet[i,1],mark[markIndex])
mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '<b', 'pb']
for i in range(k):
plt.plot(centroids[i,0],centroids[i,1],mark[i])
plt.show()
dataSet = loadDataSet("test.txt")
k = 4
centroids,clusterAssment = KMeans(dataSet,k)
showCluster(dataSet,k,centroids,clusterAssment)
|
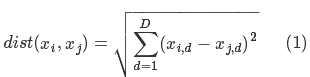
 )其计算欧式距离如下(可理解为D表示维度,i,j表示行数):
)其计算欧式距离如下(可理解为D表示维度,i,j表示行数):