DBSCAN聚类算法

一，凸集与非凸集

如下图：

左为凸集。凸集指在范围R中任意一点的连线，连线上的每一个点都在范围R里。通常这一情况都在多边形出现，所以有些说凸多边形就是这么来的。
右为非凸集，因为如图示的两点连线中，有部分点在R外头，不属于R，因此为非凸集。

二，DBSCAN原理

DBSCAN聚类算法适用于非凸数据集，而上一次的K-Means聚类算法就不怎么适用。
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一个比较有代表性的基于密度的聚类算法。与划分和层次聚类方法不同，它将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在噪声的空间数据库中发现任意形状的聚类。
如下图：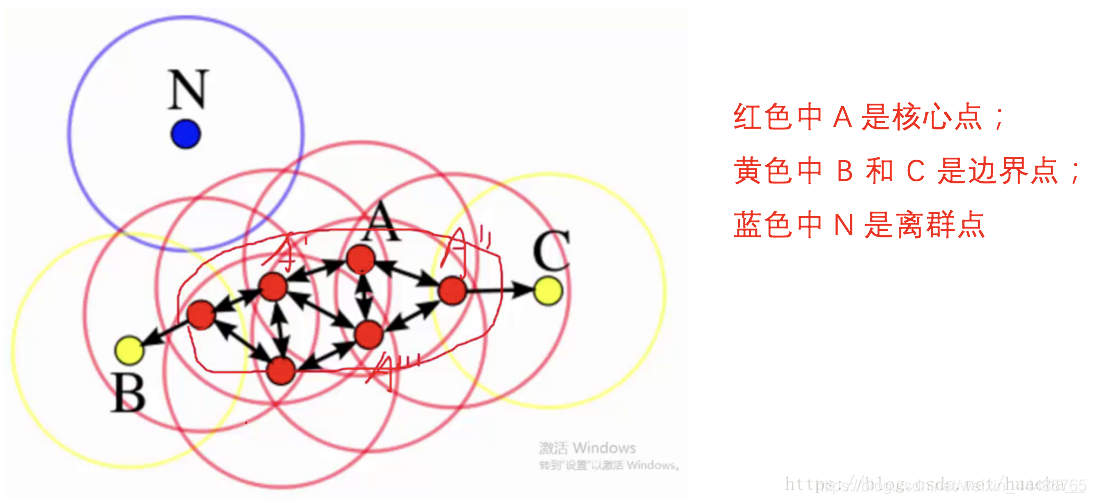

系统在众多样本点中随机选中一个，围绕这个被选中的样本点画一个圆，规定这个圆的半径以及圆内最少包含的样本点，如果在指定半径内有足够多的样本点在内，那么这个圆圈的圆心就转移到这个内部样本点，继续去圈附近其它的样本点，类似传销一样，继续去发展下线。等到这个滚来滚去的圈发现所圈住的样本点数量少于预先指定的值，就停止了。那么我们称最开始那个点为核心点，如A，停下来的那个点为边界点，如B、C，没得滚的那个点为离群点，如N。

三，参数与概念

半径（eps）：

不断对比点之间的距离d，从小至大排列，当发现d的差异变大，则选前一个d为半径。

Minptx:

圈内圈住的点个数。

Ε邻域：

给定对象半径为Ε内的区域称为该对象的Ε邻域；

核心对象：

如果给定对象Ε邻域内的样本点数大于等于MinPts，则称该对象为核心对象；

直接密度可达：

对于样本集合D，如果样本点q在p的Ε邻域内，并且p为核心对象，那么对象q从对象p直接密度可达。

密度可达：

对于样本集合D，给定一串样本点p1,p2….pn，p= p1,q= pn,假如对象pi从pi-1直接密度可达，那么对象q从对象p密度可达。

密度相连：

存在样本集合D中的一点o，如果对象o到对象p和对象q都是密度可达的，那么p和q密度相联。

可以发现，密度可达是直接密度可达的传递闭包，并且这种关系是非对称的。密度相连是对称关系。DBSCAN目的是找到密度相连对象的最大集合。

四，优缺点。

优点：

1. 与K-means方法相比，DBSCAN不需要事先知道要形成的簇类的数量。

2. 与K-means方法相比，DBSCAN可以发现任意形状的簇类。

3. 同时，DBSCAN能够识别出噪声点。

4. DBSCAN对于数据库中样本的顺序不敏感，即Pattern的输入顺序对结果的影响不大。但是，对于处于簇类之间边界样本，可能会根据哪个簇类优先被探测到而其归属有所摆动。

5. 可以在聚类的同时发现异常点，对数据集中的异常点不敏感。

6. 聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

   缺点：

7. DBScan不能很好反映高维数据。

   2. DBScan不能很好反映数据集以变化的密度。
   3. 如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差。