分类问题的本质是确定样本x属于类别ci的概率p(Ci|x)。在上周整理的分类问题中,我们采用生成式方法,借助贝叶斯公式和极大似然估计,首先计算出p(x|Ci)和p(x,Ci),然后再计算出p(Ci|x)。以二分类为例:
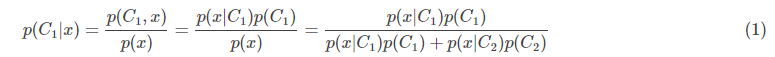
如果p(C1|x)>0.5,则将x归入类别C1;如果p(C1|x)<0.5,则将x归入类别C2。一般情况下,我们将p(x|C1)和p(x|C2)假设成服从不同μ1,μ2但是相同Σ的高斯分布。因为高斯分布是自然界中最常见的一种分布,两个分布同用一个协方差矩阵Σ有助于减少参数数目,防止过拟合。
Logistic回归推导
现在我们尝试对上述后验概率(1)进行变形
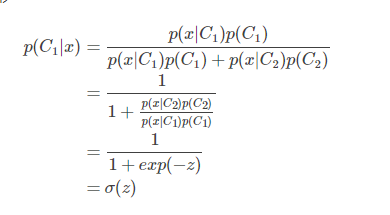 )
)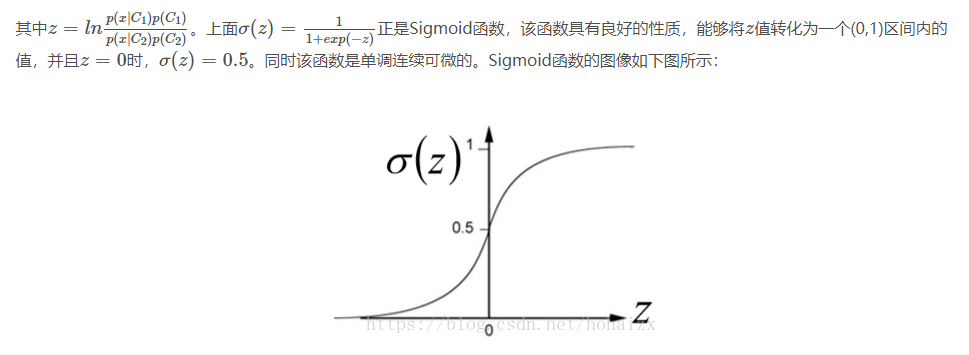
现在还需要确定的是z是什么,我们继续对z进行推导

Logistic回归损失函数


寻找最佳参数
交叉熵损失函数虽然看起来形式复杂,但是求导并不复杂
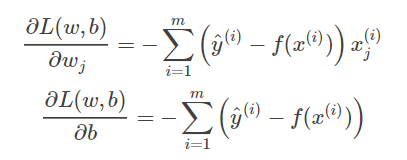
求导结果与线性回归均方误差的导数一模一样。采用梯度下降算法更新参数
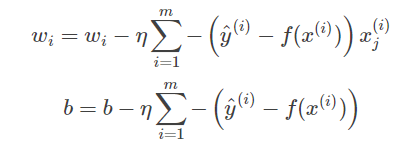
关于交叉熵损失函数与均方误差损失函数的对比可以参考下图
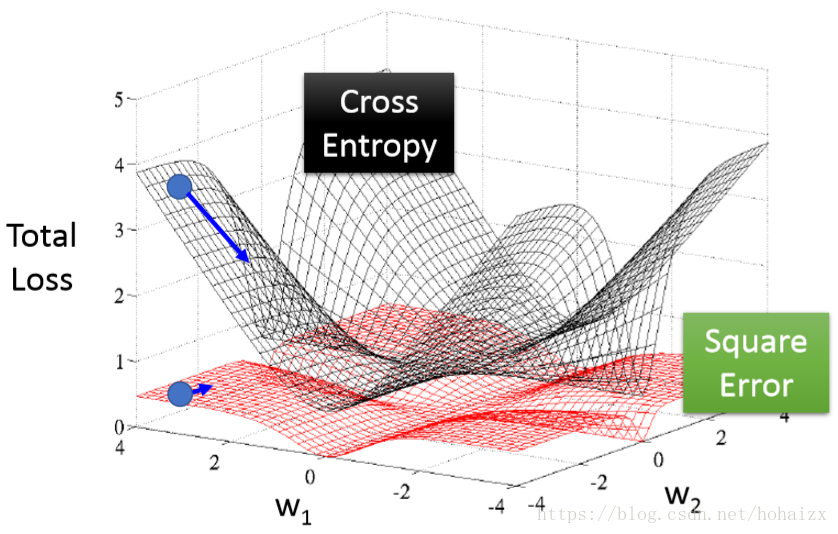
可以看出均方误差损失函数的曲面近乎是平坦的,因此梯度下降很容易停下来,而交叉熵损失函数则不会出现这个问题。
总结
Logistic回归相较于生成式模型操作简单,并且准确率也比较的高,但这并不表明Logistic回归能够解决所有的二分类问题,因为Logistic回归的分界面是一个平面,因此对于线性不可分问题,Logistic回归将束手无策,需要借助更加复杂的分类器。
参考文献
李宏毅机器学习2017年秋http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML17_2.html


