机器学习基础(4)
朴素贝叶斯(Native Bayesion)
朴素贝叶斯的特点
1.优点:在数据较少的情况下任然有效,可以处理多类别问题。
2.缺点:对于输入数据的准备方式较为敏感。
3.适用数据类型:标称型数据类型。
条件概率的计算
1.条件概率计算公式(其中A,B均表示事件特征):
$$
p(A|B)=p(AB)/p(B)
$$
2.贝叶斯准则:
$$
p(c|x)=\frac{p(x|c)p(c)}{p(x)}
$$
使用条件:已知p(x|c),要求p(c|x)
贝叶斯决策论
朴素贝叶斯是贝叶斯决策论的一部分。
假设我们用p1(x,y)表示数据点(x, y)属于类别1的概率,用p2(x, y)来表示类别2的概率,那么就可以有:
1.当p1(x, y) > p2(x, y),表示类别1。
2.当p1(x, y) < p2(x, y),表示类别2。
选择高概率事件来选择对应类别,这就是贝叶斯决策论的核心思想。
分类
通过上述对贝叶斯决策论的介绍,对应到贝叶斯准则中就可以得到:
1.当p(c1|x, y) > p(c2|x, y),那么属于类别c1。
2.当p(c1|x, y) < p(c2|x, y),那么属于类别c2。
朴素贝叶斯的一般过程
1.收集数据:任何适用方法。
2.准备数据:数值型或布尔型的数据。
3.分析数据:有大量特征时,绘制特征作用不大,使用直方图效果更好。
4.训练算法:计算不同的独立特征的条件概率。
5.测试算法:计算错误率。
6.使用算法:可以在任意的分类场景中使用朴素贝叶斯分类器。
使用python实现
1 | def loadDataSet(): |
在python.shell中检查结果:
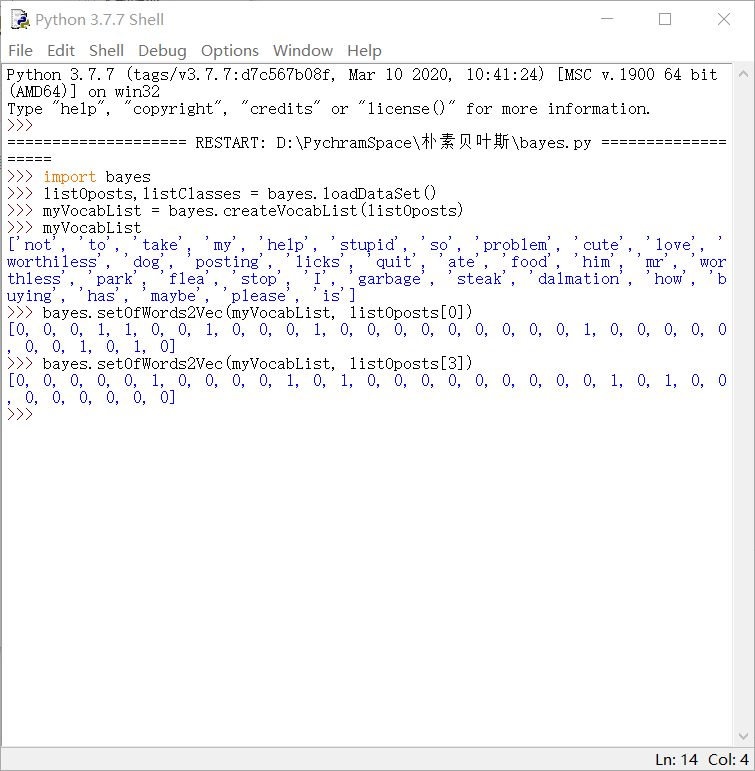
朴素贝叶斯分类器训练函数:
1 | def trainNB0(trainMatrix, trainCategory): |
检查: