摘要: 形式语言与自动机是计算机科学的理论基础,对于计算机科学与技术专业人才的计算思维能力培养极其重要。本文首先从Chomsky谱系出发,对形式语言的概念和类别进行了阐述,然后按照形式文法与自动机之间的对应关系,介绍了四种自动机。最后通过单词拼写检查例子展现了形式语言与自动机在自然语言处理中的应用。
引言
自动机和形式语言是计算机科学的理论基础,它在信息科学,生物学,管理学等众多学科领域中应用广泛。自动机和形式语言的研究起源于二十世纪人们对逻辑学的研究,1930年,图灵提出图灵机这一抽象计算模型,用以界定什么能够计算,什么不能够计算,图灵机也因此成为现代计算机的理论基础。其后,德国著名数学家Hilbert在研究证明理论时进一步推动了自动机和形式语言的研究。上世纪60年代,齐姆斯基借助形式化的方法描述语言,提出了Chomsky谱系,从而使形式语言理论成为一门独立的学科。
计算机科学与技术强调4方面的专业能力:计算思维能力、算法分析与设计能力、程序设计与实现能力、计算机系统的认知、分析、设计和应用能力。形式语言与自动机理论,在对计算机科学与技术学科人才进行计算思维能力培养中占有极其重要的地位。本文首先对形式语言和自动机的基本概念,研究内容进行讨论,然后结合目前自然语言处理的热点,展示了形式语言与自动机在自然语言处理中的应用。
形式语言
形式语言与形式文法
语言是交流和沟通的工具,分为自然语言和人工语言。自然语言是人类使用的语言,如汉语、英语等,这类语言由自然进化产生;人工语言是为特定应用而认为设计的语言,如化学家用的化学式,计算机编程语言等。不同的研究者对语言给出了不同的定义。《现代汉语词典》中对语言定义为:“人类所特有的用来表达意思,交流思想的共工具,是一种特殊的社会现象,由语音、词汇和语法构成一定的系统。”乔姆斯基将语言定义为:“按照一定规律构成的句子和符号串的有限或无限集合。”我国计算语言学家吴蔚天也给出了自己对语言的定义:“语言可以被看成一个抽象的数学系统。”这些定义描述虽然不同,但是都包含了语言是一个词汇表构成的符号系统的观念,因此可以采用数学的方法对语言的语法进行研究。在数学、逻辑和计算机科学中,将用来精确地描述语言(包括人工语言和自然语言)及其结构的手段称为形式语言,也称代数语言。1956年,乔姆斯基发表了用形式语言方法研究语言的第一篇文章,由此开启了形式语言的研究。
在形式语言学中,我们一般将语言形式化定义为:给定一组符号,称为字母表,以Σ表示,又以Σ∗Σ∗表示由Σ中字母组成的所有字符串的集合,则Σ∗的每个子集都是Σ上的一个语言。对语言就行定义后,还需要对语言进行形式化描述,形式语言学中,采用形式文法对语言进行描述。形式文法被严格定义为四元组G=(N,Σ,P,S),其中,N是非终结符的有穷集合;Σ是终结符的有限集合,N∩Σ=∅;V=N∪Σ称总词汇表;P是一组重写规则的有限集合:P={α→β},其中,α,β是V中元素构成的串,但α中至少应含有一个非终结符号;S∈N,称为句子符或初始符。在形式文法的定义中,重写规则P={α→β}最为重要,重写规则P={α→β}表示字符串α可以被改写成β。一个初始字符串通过不断运用重写规则,就可以得到另一个字符串,通过选择不同的规则并以不同的顺序来运用这些规则,就可以得到不同的新字符串。
形式语言类别
文法是一种足够强大的语言描述工具,理论上可以描述语法规则非常复杂的语言,因此需要对其加以限制才能简单充分地描述常见的语言。针对重写规则P加以不同的约束,乔姆斯基将形式文法分为以下四类:
(1)0型文法,对重写规则P不施加任何限制,因此0型文法又称作无约束文法。由0型文法产生的语言记为L(G0)。
(2)1型文法,如果P中的规则满足如下形式:αAβ→αγβ,其中A∈N,α,β,γ∈(N∪Σ)∗γ∈(N∪Σ)∗,且γ至少包含一个字符,则称该文法为1型文法,观察重写规则P可以发现,字符串A只有在上下文分别是α和β的情况下才能被改写成γ,因此1型文法又称为上下文有关文法(context-sensitive grammar,CSG)。由1型文法产生的语言记为L(G1)。
(3)2型文法,如果P中的规则满足如下形式:A→α,其中A∈N,α∈(N∪Σ)∗,则称该文法为2型文法,因为对A改写成α的规则没有上下文约束,2型文法又称为上下文无关文法(context-free grammar,CFG)。由2型文法产生的语言记为L(G2)。
(4)3型文法,如果P中的规则满足如下形式:A→Bx,或A→x,其中A,B∈N,x∈Σ,则称该文法为正则文法或3型文法。由3型文法产生的语言记为L(G3)L(G3)。
显然,每一个正则文法都是上下文无关文法,每一个上下文无关文法都是上下文有关文法,而每一个上下文有关文法都是0型文法,即L(G3)⊆L(G2)⊆L(G1)⊆L(G0)。从0型文法到3型文法,限制越来越多,但性质也越来越好。如果一种语言能由几种文法所产生,则把这种语言称为在这几种文法中受限制最多的那种文法所产生的语言。在计算机科学中最常见的是上下文无关语言和正则语言,上下文无关语言根据其转换规则可以表示成树的形式,因而可以使用图论的方法进行搜索。
自动机
自动机概念
自动机是一种抽象的计算装置,给定输入符号,自动机将依据转移函数从当前状态跳转到下一状态,逐个读取输入中的符号,直到输入被耗尽,自动机也将停止下来。依据自动机停止时的状态,可以判定这个输入是被自动机“接受”还是“拒绝”。如果自动机停止于“接受状态”,则这个输入被自动机接受,反过来,如果自动机停止于“拒绝状态”,则这个输入被自动机“拒绝”。自动机接受的所有输入的集合称为这个自动机接受的语言。1951年到1956年间,克林(Kleene)在研究神经细胞中,从识别的角度,建立了识别语言的系统——有穷状态自动机。1959年,乔姆斯基发现文法和自动机分别从生成和识别的角度去表达语言,而且证明了文法与自动机的等价性,这一成果被认为是将形式语言置于了数学的光芒之下,使得形式语言真正诞生了。
自动机分类
基于乔姆斯基建立的形式文法与自动机之间的联系,我们也可以将自动机分成四种类型:有限自动机,下推自动机,线性有界自动机和图灵机,并与形式文法一一对应:若某一语言能用有限自动机识别,则它能用正则文法生成,反之亦然;若某一语言能用下推自动机识别,则它能用上下文无关文法生成,反之亦然;若某一语言能用线性有界自动机识别,则它能用上下文有关文法生成,反之亦然;若某一语言能用图灵机识别,则它能用0型文法生成,反之亦然;
有限自动机与正则文法
有限自动机M可以用五元组表示M=<Σ,Q,δ,qo,F>:
Σ:输入符号的有穷集合;
Q:状态的有限集合;
qo∈Q是初始状态;
F:终止状态集合,F⊆Q;
δ是Q与Σ的值积Q×Σ到Q(下一个状态)的映射。它支配着有限状态控制的行为,有时也称状态转移函数。
有限自动机示意图如下: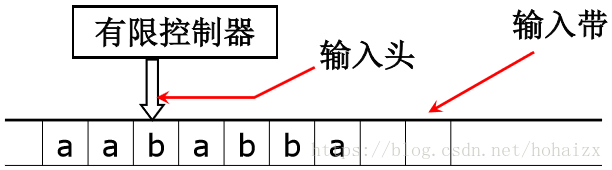
处在状态q∈Q中的有限控制器从左到右依次从输入带上读入字符。开始时有限控制器处在状态qo,并注视Σ∗中一个链的最左符号。映射δ(q,a)=q′(q,q′∈Q,a∈Σ)表示在状态q时,若输入符号为a,则自动机进入状态q′,并且将输入头向右移动一个字符。
映射δ(q,a)=q′可以由状态转换图描述。
为了明确起见,终止状态用双圈表示,起始状态用有“开始”标记的箭头表示。
有限自动机分为确定有限自动机(definite automata,DFA),不确定有限自动机(non-definite automata,NFA),NFA与DFA的唯一区别是:在NFA中δ(q,a)是一个状态集合,而在DFA中δ(q,a)δ(q,a)是一个状态。如果L是一个被NFA所接受的句子的集合,则一定存在一个DFA,它能够接受L。若G=<VN,VT,P,S>是一个正则文法,则存在一个有限自动机M=(Σ,Q,δ,q0,F),使得:T(M)=L(G)。反之亦然。由G构造M的一般步骤如下:
(1)令Σ=VT,Q=VN∪T,q0=S,其中T是一个新增加的非终结符。
(2)如果在P中有产生式S→ε,则F=S,TF=S,T,否则F=T。
(3)如果在P中有产生式B→a,B∈VN,a∈VT,则T∈δ(B,a)。
(4)如果在P中有产生式B→aC,B,C∈VN,a∈VT,则C∈δ(B,a)。
(5)对于每一个a∈VT,有δ(B,a)=∅δ(B,a)=∅。
由M构造G的一般步骤如下:
(1)令VN=Q,VT=Σ,S=q0;
(2)如果C∈δ(B,a),B,C∈Q,a∈Σ,则在P中有产生式B→aCB→aC;
(3)如果C∈δ(B,a),C∈F,则在P中有产生式B→a。
线性有界自动机与上下文有关文法
线性有界自动机(Linear Bounded Automata,LBA)是一种确定的单带图灵机,其读写头不能超越原输入带上字符串的初始和终止位置,即线性有界自动机的存储空间被输入符号串的长度所限制。其意义是给定一个字符串,只准修改,不准添加删除,但是修改可以随意修改。
各类自动机的主要区别是它们能够使用的信息存储空间的差异:有限状态自动机只能用状态来存储信息;下推自动机除了可以用状态以外,还可以用下推存储器;线性有界自动机可以利用状态和输入/输出带本身,因为输入/输出带没有“先进后出”的限制,因此,其功能大于栈;而图灵机的存储空间没有任何限制。


