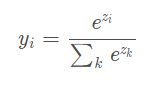使神经网络具有记忆力——RNN及LSTM

不依靠第三方库（除了numpy）实现一个神经网络

现在各种机器学习、深度学习第三方库都有非常成熟高效的神经网络实现，借助这些第三方库，短短几行代码就能实现一个神经网络。但是对于一个机器学习/深度学习的入门者来说，这些代码封装得太过彻底，往往一行代码就能实现BP算法或者梯度下降算法，这导致很多初学者即使掌握了繁复的数学推导后，依旧对神经网络的工作流程没有一个直观的认知。在我看来，自己动手实现一个神经网络，包括BP算法，梯度下降算法等，是将理论应用于实践的最佳尝试。

实验整体介绍

本次实验将在MNIST数据集上进行，MNIST是一个0-9手写数字数据集，每个样本是28*28的灰度图。官方数据集包含训练样本60000条，测试样本10000条，下面是一些手写数字样例：

本实验没有选择官网上的数据集，而是选择deeplearning.net上公布的数据集，其将数据集分成了训练集、验证集和测试集，其大小分别是50000，10000，10000，同时将样本的每个像素值归一化到[0,1]之间了。因此可以确定模型的输入是784维；输出是10维，对应每个数字的概率。显而易见，这是一个多分类问题，可以采用Softmax回归对输入特征进行分类。

Softmax回归

计算模型输出

首先从最简单的Softmax回归开始，我们不对输入向量进行任何特征提取，直接利用Softmax回归对其进行分类，如下图所示：

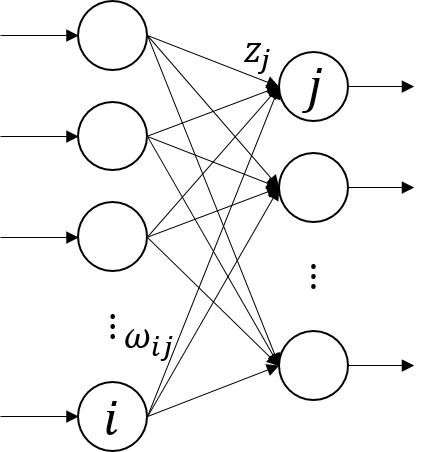
因此，可以写出Softmax回归的数学表达式：
y=softmax(xw)

其中，w是模型的权重，大小为78410，x是输入，大小为m784，y是输出，大小为m*10。

将Softmax函数展开，如下图所示：

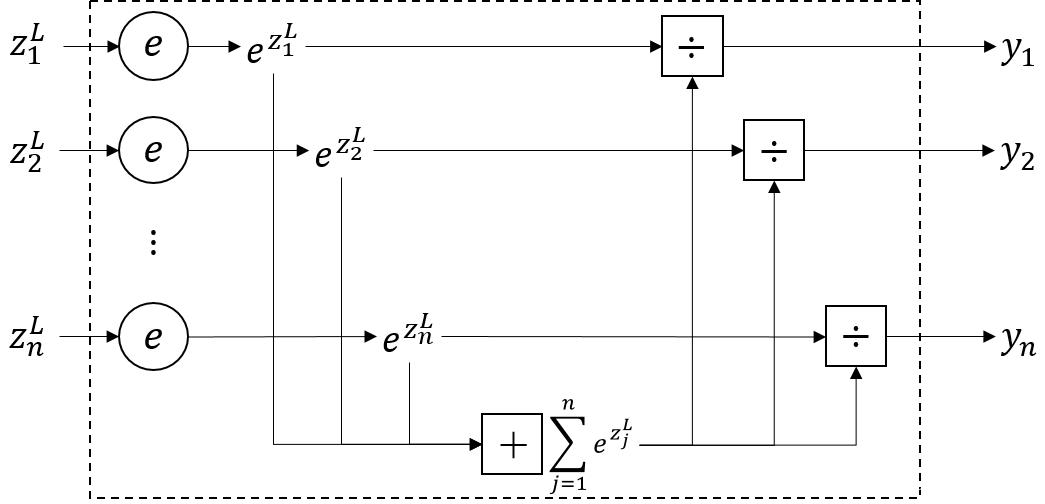
其中，虚线框内就是Softmax函数的处理过程，可以看到，Softmax函数形式如下：

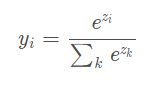
因此，Softmax回归代码表示如下：

def SoftmaxRegression(x, w):
    z = np.dot(x, w)
    e = np.exp(z)
    y = (np.transpose(e) / np.sum(e, axis=1)).T

计算模型损失

损失函数选择负对数似然函数，也即最大似然估计，因此损失函数的数学表达式是：
C=−logyr

yr是样本标签r对应的预测概率值，以手写数字识别为例，假设某样本对应的真实标签是3，而神经网络预测样本是3的概率为yr，显然yr越接近于1，网络预测得越准，反之yr越接近于0，网络预测越不准，给予的惩罚也应该越大，负对数似然函数恰好满足该性质。

因此，负对数似然代价代码表示如下：

def negative_log_likehood(p_y_given_x, y):
    return -np.mean(np.log(p_y_given_x)[np.arange(y.shape[0]), y])

“p_y_given_x”是模型的输出，表示样本属于每个标签的概率，”y”是样本真实标签。

接着是最小化损失，得到最优模型参数。计算损失函数的最小值采用的是梯度下降算法，其需要计算损失函数在www处的梯度值。

模型构建与优选

通常，我们在训练集上训练模型，更新模型参数，在验证集上对模型性能进行验证，当模型在验证集上的性能达到要求时，得到的模型就是最优模型，然后在测试集上测试模型。

def build_model(datasets, w_initial, alpha, n_epochs, epsilon, batch_size):
    W = w_initial
# 训练集，验证集，测试集
train_set_x, train_set_y = datasets[0]      
valid_set_x, valid_set_y = datasets[1]
test_set_x, test_set_y = datasets[2]

# 将数据集分成较小的batch
n_train_batches = train_set_x.shape[0] // batch_size     # 训练集划分成batch数目

# 模型训练
best_valid_cost = 0
validation_frequency = 100   # 梯度下降迭代validation_frequency次，在验证集上验证一次模型性能
epoch = 0
done_looping = False
while (epoch < n_epochs) and (not done_looping):
    epoch += 1
    for batch_index in range(n_train_batches):
        x = train_set_x[batch_index * batch_size: (batch_index + 1) * batch_size]  # 每次训练的x
        y = train_set_y[batch_index * batch_size: (batch_index + 1) * batch_size]  # 对应的y
        # 训练模型
        W, cost_train = gradient_descent(x, y, W, alpha, L1_reg, L2_reg)
        # 验证模型
        cost_valid, error_num_valid = valid_model(valid_set_x, valid_set_y, W)
        this_validation_loss = error_num_valid / valid_set_x.shape[0]       # 错误率
        
        num_iter = (epoch - 1) * n_train_batches + batch_index
        if num_iter % validation_frequency == 0:
            # 跟踪验证集上性能变化
            print("梯度下降迭代%d次后，验证集上误差为：%f，准确率为：%f%%" % (num_iter, cost_valid, (1 - this_validation_loss) * 100))
        
        # 判断是否early stopping
        if abs(cost_valid - best_valid_cost) < epsilon:
            done_looping = True
            print("验证集上误差不再下降，模型训练结束")
            break
        else:
            best_valid_cost = cost_valid
          
if not done_looping:
    print("达到最大epoch次数，模型训练结束")

# 模型测试
test_precision = test_model(test_set_x, test_set_y, W)
print("测试集上模型准确率为：%f%%" % (test_precision * 100))

总结

以上实现了一个最简单的Softmax回归和神经网络，上面只贴出了主要步骤的代码实现，完整的代码可以在下面这个链接下载，代码在linux环境下实现，如有问题，欢迎多多交流！