元胞自动机原理

一.概念

元胞自动机(cellular automata，CA) 是一种时间、空间、状态都离散，空间相互作用和时间因果关系为局部的网格动力学模型，具有模拟复杂系统时空演化过程的能力。
元胞自动机可用来研究很多一般现象。其中包括通信、信息传递(Communication)、计算(Compulation)、构造 (Construction)、材料学(Grain Growth)、复制 (Reproduction)、竞争(Competition)与进化(Evolutio，])等(Smith A.,1969;Perrier，J.Y.,1996)。同时。它为动力学系统理论中有关秩序 (Ordering)、紊动 (Turbulence)、混沌 (Chaos)、非对称(Symmetry-Breaking)、分形(Fractality)等系统整体行为与复杂现象的研究提供了一个有效的模型工具 (Vichhac。G，1984; Bennett，C,1985)。

元胞自动机自产生以来，被广泛地应用到社会、经济、军事和科学研究的各个领域。应用领域涉及社会学、生物学、生态学、信息科学、计算机科学、数学、物理学、材料学、化学、地理、环境、军事学等。

二.描述

标准元胞自动机是一个由「元胞、元胞状态、邻域和状态更新规则」构成的四元组，用数学符号可以表示为A=(L,d,S,N,f)

A代表一个元胞自动机系统
L表示元胞空间
d表示元胞自动机内元胞空间的维数，是一正整数
S是元胞有限的、离散的状态集合
N表示某个邻域内所有元胞的集合
f表示局部映射或局部规则。

1. 元胞空间
   元胞是构成元胞自动机的最基本单元，而元胞空间是元胞所分布的空间网点集合。
   理论上，元胞空间是在各维向上无限延展的，但实际中无法在计算机上实现。因此，需要定义不同的边界条件。
   元胞空间的边界条件主要有三种类型：周期型、反射型和定值型。
2. 元胞状态
   通常在某一个时刻一个元胞只能有一种元胞状态，而且该状态取自一个有限集合，如{0,1}，{生,死}或{0,a1,a2,an}。
   在社会科学领域中，元胞状态可以用来代表个体所持的态度、个体特征或行为等。
3. 邻域
   在空间位置上与元胞相邻的细胞称为它的邻元，由所有邻元组成的区域称为它的邻域。
   在一维元胞自动机中，通常以半径r来确定邻域，距离某个元胞r内的所有元胞均被认为是该元胞的邻域。

1.一维元胞自动机的邻域：

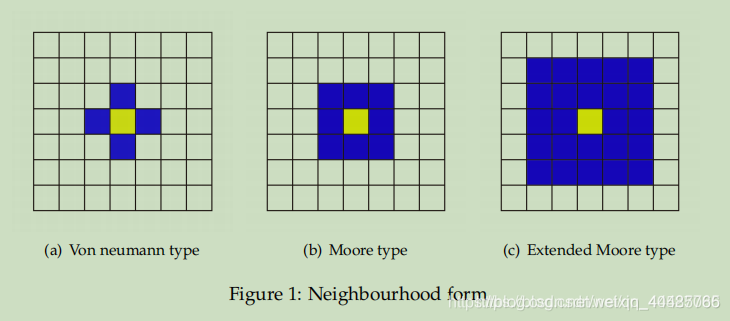
2.在二维元胞自动机中，通常有以下几种类型的邻域：

1. 冯·诺依曼型(vonNeumanNeighborhoods)
   2. 摩尔型(MooreNeighborhoods)
   3. 马哥勒斯型(MargolusNeighborhoods)
      它是每次将一个2×2的元胞块做统一处理，而上述前两类邻域中，每个元胞是分别处理的

三.生命游戏机

1． 如果一个细胞周围有3个细胞为生（一个细胞周围共有8个细胞），则该细胞为生（即该细胞若原先为死，则转为生，若原先为生，则保持不变） 。

2． 如果一个细胞周围有2个细胞为生，则该细胞的生死状态保持不变；

3． 在其它情况下，该细胞为死（即该细胞若原先为生，则转为死，若原先为死，则保持不变）。

function ca
m=30;n=30;p=.7;h=100;
for x=1:m
for y=1:n
r=rand(1);
if r>p
a(x,y)=1;
else a(x,y)=0;
end
end
end
for x=1:m
for y=1:n
if a(x,y)==1
fx=[x-1,x-1,x,x];fy=[y-1,y,y,y-1];fill(fx,fy,'g'),hold on
else
end
end
end
for k=1:h
fx=[0,m,m,0];fy=[0,0,n,n];fill(fx,fy,'k'),hold on
for x=2:m-1
for y=2:n-1
b(x,y)=a(x-1,y-1)+a(x-1,y)+a(x-1,y+1)+a(x,y-1)+a(x,y+1)+a(x+1,y-1)+a(x+1,y)+a(x+1,y+1);
if b(x,y)==2,c(x,y)=a(x,y);
elseif b(x,y)==3,c(x,y)=1;
else c(x,y)=0;
end
end
end
c(1:m,1)=a(1:m,1);c(1:m,n)=a(1:m,n);
for x=1:m
for y=1:n
if c(x,y)==1
fx=[x-1,x-1,x,x];fy=[y-1,y,y,y-1];fill(fx,fy,'g'),hold on
else
end
end
end
pause(.05)
a=c;
end